Introduction

A seismic analysis of the existing West Bay Crossing of the San Francisco - Oakland Bay Bridge was performed for the California Department of Transportation to determine the seismic vulnerability and retrofitting requirements of the structure. Engineering studies were performed to gain an understanding of the dynamic seismic behavior of the bridge, to evaluate its seismic vulnerability, and to determine basic retrofit requirements. The goals and scope of the evaluation, along with the methods and findings of the engineering studies that were performed to evaluate seismic vulnerability, are summarized here.

The 8.25 mile long San Francisco-Oakland Bay Bridge provides the only direct highway link between San Francisco and the East Bay communities. Since it first opened to traffic in 1936, it has been a critical structure to the people of the San Francisco Region and the State of California. It was recognized by the American Society of Civil Engineers (ASCE) in 1955 as one of the seven wonders of the United States. From its west end in San Francisco to its east end in Oakland, it consists of the San Francisco Approaches, the West Bay Crossing, the Island Crossing, the East Bay Crossing, and the East Bay Approaches.

The evaluation made use of separately contracted site-specific seismic hazard assessment and ground motion studies [2,3], and consisted of a number of engineering studies designed to evaluate the elastic and inelastic mechanical properties of the bridge and its principal components, estimate the seismic response and structural behavior of the bridge in earthquakes of differing magnitudes, determine the damage that might occur to the bridge in these earthquakes, estimate the vulnerability of the bridge to collapse or loss of service due to this damage, and provide an estimate of the retrofitting measures that would be required to keep the bridge open for continued service after a major earthquake. These studies provided one step in the ongoing seismic retrofit program of this heavily used transportation structure.

Bridge Description

The West Bay Crossing (Fig. 1), connecting Yerba Buena Island and the City of San Francisco, consists of back-to-back suspension bridges with main spans of 2,310 ft (704 m), side spans of 1,160 ft (354 m), and western continuous truss approach spans, for a total length of 10,300 ft (3,140 m). The riveted steel stiffening trusses that carry ten lanes of traffic on two 66 ft (20m) wide roadway levels, are suspended from two 28¾ in. (0.73 m) diameter parallel wire cables. Braced steel towers up to 470 ft (143 m) tall are founded on multicellular concrete caissons up to 231 ft (70 m) deep that are embedded in soil and bear directly on rock. With its 1.95 mile (3.14 km) long cables between end-anchorages, the 59-year-old West Bay Crossing is one of the longest continuous elevated structures in the United States.

Fig. 1: Bridge Elevation

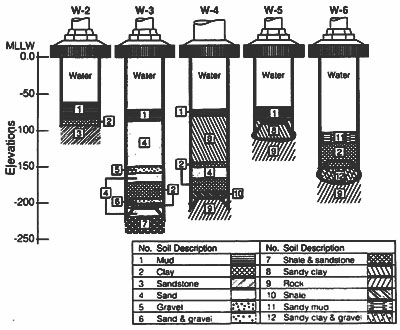
Fig. 2: Foundation Conditions

The anchorages and Piers W1 through W6 are founded on Franciscan sandstone. Soil conditions at Piers W2 - W6 are shown in Fig. 2. Foundations at Piers W3 - W6 are cellular concrete caissons that were floated to the site, sunk through the overlying soil to rock, and then sealed with tremie concrete. These caissons extend as far as 231 ft (70 m) below water level and have footprints as large as 92 ft x 197 ft (28 m x 60 m). The caissons are lightly reinforced with low-deformation bars. Foundations at Piers W1 and W2 are spread footings on rock, built inside cofferdams. Piers A and B that support the continuous truss spans are founded on spread footings that bear on sand.

The San Francisco cable anchorage consists of massive concrete blocks keyed into the rock. The center anchorage at W4 is a 450 ft (137 m) high vertical cantilever pier, with the cables anchored to steel A-frames inside its walls. At the Yerba Buena Island anchorage, the cables are anchored in grillage beams at the bases of 170 ft (52 m) grouted tunnels.

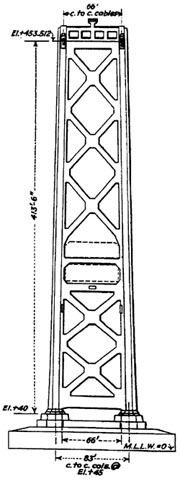
Fig. 3: Typical Tower

Batter-leg steel towers (Fig. 3) support the cables at W2, W3, W5, and W6. Riveted splices in the tower shafts were designed to develop the full compression capacity of the plates, but only partial tension capacity. The tower shafts are connected to the caisson caps with bolts anchored in steel grillages in the concrete. These bolts are not capable of developing the full bending capacity of the tower shafts. Additional support for the cables is provided by steel bents at W1 and the Yerba Buena anchorage. Cast steel cable saddles are bolted to the top of each tower and cable bent.

A 35 ft (10.7 m) deep suspended steel stiffening truss system (Fig. 4) supports the upper and lower deck slabs. Steelwork consists of top and bottom chords, truss posts, diagonals, floor beams, and lower deck transverse K-bracing. Expansion joints are provided at each tower. The floor systems consist of concrete slabs supported on steel stringers and the floor beams. The trusses are supported by the suspenders and by rocker posts at the towers. Longitudinal restraint is provided only by pendulum action of the cable system. Transverse restraint is provided through wind locks at the towers in the bottom chord plane. The continuous spans make use of a traditional truss system with a similar layout.

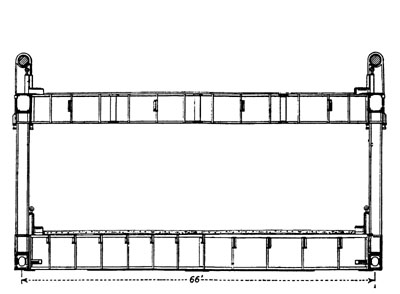
Fig. 4: Stiffening truss section

The 1940 paper Earthquake Stresses in the San Francisco-Oakland Bay Bridge [4], outlines the approach used in the original seismic analysis and design of the bridge. The earthquake forces used were "those resulting from a ground motion with a horizontal acceleration of 0.1 g, a period of 1.5 sec., and an amplitude of 2.2 inches". The estimated 5 to 15 sec. vibration period of the superstructure was considered long enough that an earthquake could never be in resonance with any part of the structure. For the towers, it was assumed that a 0.1 g acceleration acted at the center of the towers mass, with analogous participation from the adjacent spans. The overall conclusion with respect to seismic resistance was that the earthquake stresses were of the same order as those arising from the assumed wind loads, thus very little additional material was provided to resist earthquake forces.

Project Goals and Strategy

The contracted goals of the project were to evaluate the anticipated seismic performance of the West Bay Crossing by performing a seismic analysis of the bridge using ground motions provided by Caltrans, and to make recommendations and cost estimates for seismic retrofit measures. The project strategy adopted to meet these goals within the imposed time and budget constraints consisted of the following tasks:

1. Development of linear and nonlinear global computer models of the bridge, to account for the dynamic properties of the superstructure and substructure, and interaction between the foundations and the surrounding soil. This task entailed development of three-dimensional global structural models capable of capturing dominant linear and nonlinear seismic response of the system.

2. Development of component models as necessary to determine critical local responses. These models, including soil-structure interaction (SSI) models of the foundations, detailed nonlinear inelastic finite element models of bridge subassemblies, and simple models of members and connections based on fundamental principles, provided a basis for defining mechanical properties used in the global models.

3. Analysis of these models under ground motion input to determine critical bridge response. The analyses included linear response spectrum analyses, plus linear and nonlinear time-history analyses with multi-support incoherent ground motion input. Linear analyses were performed first; then, as "important" response nonlinearities were found, they were explicitly incorporated in the models and analyses.

4. Determination of demand and capacity values for forces and deformations at critical locations. Demands and capacities were expressed in terms of displacements, focusing on the ability of systems and elements to withstand the deformation or ductility demands imposed by the earthquake. Structural vulnerability was evaluated on the basis of these demands and capacities.

5. Preparation of recommendations for any retrofit construction required to enable the bridge to perform satisfactorily during the specified earthquakes. Preparation of approximate construction cost estimates for the recommended retrofit work.

It was recognized by OPAC at the inception of the project that the engineering analyses required to reach the stated goals would by necessity be of a predictive nature. The overall analytical approach was therefore designed to estimate the true structural response and behavior of the bridge, including explicit consideration of nonlinear global system behavior and cyclic inelastic component behavior in critical components. It was felt that this would provide a rational and most readily defensible approach to assessing vulnerability.

Performance Criteria

Caltrans Policy

Technical Approach

Development of the component performance criteria was displacement driven, focusing on the ability of the systems and elements of the bridge to withstand the deformation or ductility demands imposed by the ground motions. The Caltrans policy presented above were therefore interpreted to place the following limitations on structural deformations in the Safety Evaluation event:

1. The global structural system must be capable of accommodating the expected seismic deformations without significant loss of its gravity load carrying capability.

2. Damage to individual elements resulting from the expected deformations must be repairable without complete interruption of the bridge operation.

Rational application of such criteria, where vulnerability is assessed by comparing computed deformations with acceptable deformations, would require global modeling of all important geometric and material nonlinearities. Such analysis was judged unfeasible for this study because of the size of the bridge and the bridge model, the uncertainties in modeling the post-elastic behavior of all members and connections, and the need to predict vulnerability prior to expending the effort required for such a fully nonlinear analysis.
A simplified global modeling approach was adopted instead, in which only certain critical components were modeled as inelastic. These components were characterized as inelastic in the global model (to provide deformation demands) as well as in local subsystem models (to define deformation capacities). For the majority of components, surrogate elastic deformations and forces were compared with surrogates of allowable ductility ratios, based on the equal deformations assumption. Acceptable strength demand/capacity ratios were established for these components based on their ductility characteristics and consequences of failure.

Deformation capacities of components were categorized as related to form, function, and behavior. The failure modes to which an element is susceptible, i.e. its behavior, are dictated by its form and function; its capacity depends on its behavior and form; and the consequences of failure are dictated by its function and behavior.

Form describes the material characteristics and element shapes of the component. The material type determines the shape of the stress strain curve which, along with the element geometry, defines the potential failure modes and inelastic behavior characteristics of the component.

Function describes the role the element fills in the system. The structure is considered functional only if the primary gravity load paths are complete and the elements that form these paths are not compromised. The criteria therefore distinguish between Criticality Classes of components, according to the consequences of their failure. For Criticality Class I elements, whose failure may imperil the stability of the gravity load system, inelastic deformations are acceptable only if they result in no strength loss. For Criticality Class II elements, including all other structural components, inelastic deformations are acceptable if they cause not more than 20% strength loss. Deformations must also be controlled to the extent that they do not render the bridge completely dysfunctional or un-repairable.

Behavior describes the inelastic characteristics of the element. For ductile components, including adequately braced compact steel beams in flexure and steel tension elements that yield at the gross cross section, allowable deformations are controlled by stability and reparability issues. For brittle components that may not yield prior to failure, including connections subject to net section fracture, shear failure in pre-1970's reinforced concrete, and non-compact compression elements, deformations are limited to less than those at failure. For intermediate failure modes in which the member "softens" as displacements increase, including compact sections in compression and structural systems that are susceptible to P-Δ effects, deformations are limited to values at which 80% of yield strength is maintained.

Rock Motion

Rock motions were developed under a separate Caltrans contract [2,3]. A probabilistic seismic hazard assessment provided equal-hazard spectra (Fig. 5) for 300-year and 1000-2000 year return periods used in response spectrum evaluations. A deterministic approach was used to develop target (84th percentile) response spectra for a Maximum Credible Event (Mw = 8) on the San Andreas Fault at a distance of 15 km from the bridge (Fig. 6). The rock motions used in time history analyses were generated to be compatible with these spectra.

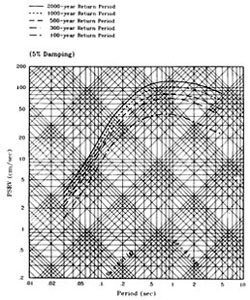
Fig. 5: Equal-hazard spectra

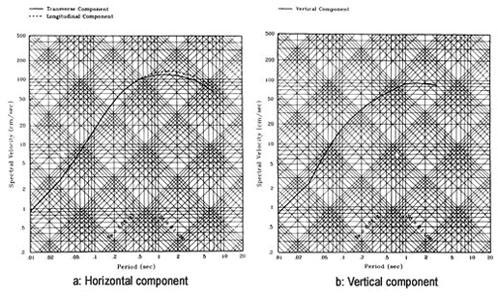
Fig. 6: Target response spectra for San Andreas event

Wave passage and incoherence effects were considered in development of multi-support histories of rock motions for the Maximum Credible Event. The multi-support motions were developed from the spectrum compatible ground motion histories using semi-empirical coherency functions and time-shifting.

Overview of Analytical Modeling

Numerous analytical models of the West Bay Crossing and its subassemblies and components were developed as a part of the vulnerability evaluation. These models are conveniently classified as either global or local. The global models were developed to capture the overall linear and nonlinear seismic response of the bridge under multi-support ground motions. The local models were developed for improved evaluation of both the demands and capacities. For the demand evaluation, pre-global modeling of local components was used to develop simplified representations of the elastic and inelastic mechanical properties of critical components that could then be incorporated into the global model. For the capacity evaluation, post-global modeling of local components was used to gain an improved understanding of the deformation limits under which the performance criteria would be met. In most cases, the same numerical description was used for both pre- and post- global models, only the driving functions changed.

Global Modeling

Global models of the West Bay Crossing were developed for evaluation of overall seismic response, including dynamic displacements as well as load and deformation demands, under multi-support seismic ground motion. The global model represented the entire bridge above the rock line, from anchorage to anchorage. Initial model development was limited to linear elastic dynamic behavior. During the engineering studies, numerous nonlinearities were incorporated into the model, to provide a better assessment of dominant response.

As well as accounting for the dynamic properties of the superstructure and substructure, the global model (Fig. 7) accounted for soil-structure interaction (SSI) between the foundations and the surrounding soil by incorporating the results of soil-structure interaction analyses. The SSI analyses were considered as local subsystem analyses; the foundations were incorporated into the global model as super-elements. Other local subsystems subjected to such analyses include the anchorage housings, truss systems, tower bases, and Pier W-1.

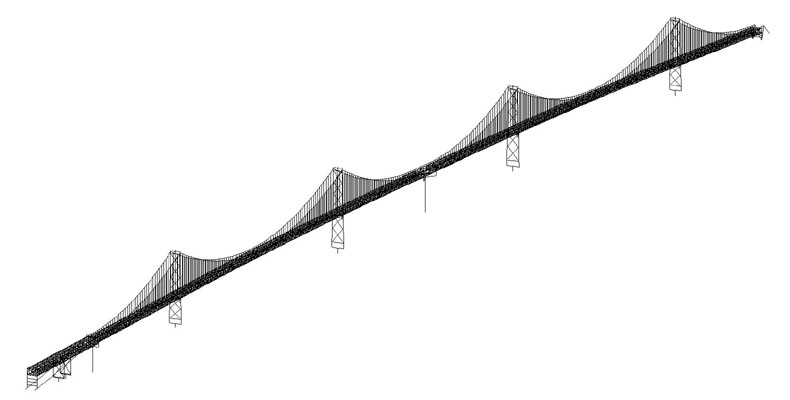
Fig. 7: Global structural model

The global model included representations of all major structural components of the bridge: the cables, the suspenders, the main towers, their supporting caissons, the continuous truss system between the San Francisco Anchorage and Pier W-1, the stiffening trusses, the center anchorage, the cable bents, etc. The following element types were used for modeling the various components of the bridge:

1. The cables and suspenders were modeled with two-node cable elements in which, for nonlinear analyses, the equilibrium equations were established using large displacement / small strain theory, and the suspenders were considered to have no compressive stiffness, to account for slackening. Over most of their lengths, the cables were modeled with axial stiffness only. Near the supports, however, the cable bending stiffness was also incorporated; this was particularly important for capturing demands on the cable bents. The geometric stiffness (initial stress) term was included in linear and nonlinear analyses. Dead load stresses and geometry were evaluated using cable theory in a separate analysis, based on a construction sequence that leaves the chords and diagonals of the stiffening trusses stress-free under dead load.

2. The trusses were modeled with each main member represented by a separate element, i.e. an equivalent line-element was not used. This was essential for capturing the distortional behavior of the un-braced double-deck system. All steel members except the floor beams were modeled with axial-force-only elements, to capture dominant behavior with reasonable numerical effort. "Pseudo sway bracing" members were incorporated to capture the distortional stiffness. In the nonlinear analyses, the truss element equilibrium equations were established in the deformed coordinate system. At each floor beam, the model has three nodes across each deck to capture the mass distribution across the widths of the top and bottom planes. Floor beams were modeled as beam-column elements with end moment releases at the stiffening truss planes. Their sectional properties were adjusted to account for shear transfer mechanisms between the deck slab and the chord members.

3. Global participation of the deck slabs was considered using frame elements, representing the gross stiffness of the floor slab / stringer system, connected to the center nodes of the floor beams. This model was calibrated against the results of a detailed local truss model described subsequently. The deck slab joints at every fourth floor beam were considered using conventional tension and compression models. Explicit modeling of pounding of these joints was outside the scope of the project.

4. The steel towers, bents A and B, the cable bents, and the A-frame in the Center Anchorage were modeled explicitly with three-dimensional frame elements. For nonlinear analyses, the frame elements utilized a large displacement, small incremental rotation, small strain formulation. The tower shafts, cable bents, and piers that are under dead load compression were formulated with geometric stiffness included. The torsional properties of the multi-cellular tower shafts were found by solving the statically indeterminate multi-cellular torsion problem. For the laced bending members, the influences of strains in the lacing bars were incorporated into the evaluations of stiffness and strength by using virtual work to evaluate equivalent line-element properties.

5. Rocking (edge uplift) of the bases of the tower shafts was modeled using frame elements with a filamented cross section. An elastic-plastic material model was used for each filament, with nominal capacity in compression and zero capacity in tension. The hold-down bolts were modeled with additional filaments.

6. Pounding of the wind locks and expansion joints between the trusses and the towers was modeled with multi-linear contact-impact gap elements. To account for the additional energy dissipation through damage that occurs during pounding, the stiffness-proportional damping of these gap elements was increased tenfold over the nominal stiffness-proportional damping assumed for the bridge system analysis.

7. The San Francisco Anchorage, Pier W1, the Center Anchorage, and the Yerba Buena Anchorage were modeled as simple equivalent frames, adequate for capturing the demands on these components due to global bridge behavior. Local analyses of these components were conducted to support the global models.

8. Foundation impedances representing the footings and caissons, were provided as boundary elements at all locations where the bridge is supported. These impedances consist of stiffness, mass, and damping matrices, derived to account for the interaction of the structure with the surrounding soil and water.

The underlying philosophy in developing this 17,000 DOF model was to provide adequate detail to capture the global and regional behavior modes of the bridge. The authors believe that any simplification of this model would have compromised its predictive ability, and that any further refinement would not have yielded results that could be interpreted within the context of the limited-scope vulnerability evaluation.

Global Analysis

Numerous analyses of the global model were undertaken to calibrate it against previous static solutions, and to evaluate live load demands, vibration properties, and seismic response.

Static Calibration

The global model was subjected to several static loadings, for which displaced shapes were provided in the original design drawings, and that represent approximately the original design traffic live loads and the wind loads on the stiffening trusses. These analyses were used only to validate the computer model, they were not used to establish demands for use in the seismic evaluations. Truss displacements based on both linearized small-displacement, and nonlinear large-displacement analyses checked very closely with the designers' values. The nonlinear analyses provided slightly smaller displacement estimates than the linear analyses; the differences were very small for the vertical loads, and were indistinguishable for the transverse loads.

Live Load Analyses

Live loads cause the dominant service load demands on the trusses, therefore static moving-load analyses were conducted to evaluate design live load demands on the truss members. In recognition of the conservatism of AASHTO lane loads for long span bridges [6], and in lieu of developing a site-specific live load model, the lane loadings specified by Caltrans for engineering studies of the Benicia-Martinez [7] and Carquinez parallel spans were used. A lane load of 0.54 kips/ft/lane was adopted, with no point loads for moment or shear, and no reduction for multiple lanes. This provided a total live load of 6.48 kips/ft to represent 12 lanes. Unfactored live load stress envelopes for truss top chords and diagonals are shown in Fig. 8. These envelopes indicate that design live load demands can utilize a significant portion of the truss member capacities.

Fig. 8: Truss live load stresses (ksi) vs. distance (ft) from center anchorage

Vibration Mode Analyses

Eigenvectors and eigenvalues were extracted for use in response spectrum analyses and to gain an understanding of the dynamic behavior of the bridge. The calculated periods and mode shapes for several key modes are shown in Fig. 9. The long period of the fundamental mode, associated with transverse motion of the main span, is characteristic of suspension bridges. None of the modes shown causes significant motions in the towers or piers. These components are stiffer than the suspended system, and are excited by higher modes. The west suspension unit has marginally longer periods due to the long anchor spans of the cables at its west end.

Fig. 9: Vibration mode shapes and periods

An ambient vibration survey conducted shortly after the bridge was built [8] indicated main span transverse periods of about 9 seconds. The original authors state in the publication that the measurements may have been in error. Considering the accuracy with which the current modeling replicates the designers' static analyses, it was concluded that the current analyses adequately represent the structural dynamics of the bridge.

Response Spectrum Analysis

Response spectrum analyses were conducted for both the 300-year event and the maximum credible event, to establish an initial probabilistic estimate of seismic demands, to eliminate modeling problems prior to the time history analyses, and to establish the importance of various dynamic modes on seismic response. About 400 eigenvectors were required to excite the supporting components of the bridge and capture 90% of their mass; this number of vectors reached a shortest modal period of about 0.3 seconds.

Results of all seismic demand analyses, based on these response spectra analyses as well as the time history analyses are discussed below:

Linear uniform support excitation time history analysis

Linear uniform-support ground motion analyses provided a starting point in refining estimates of response and seismic demands. The San Francisco Anchorage rock accelerations were input through the foundation impedances at each support. This analysis provided an improved estimate of pounding susceptibility at the tower truss joints, since peak tower responses occur earlier during the earthquake than peak truss responses.

All time history analyses were performed by direct integration of the coupled equations of motion of the bridge model. Rayleigh damping was used, with assumed damping ratios of 5% at a period of 0.2 sec and 3% at a period of 8 sec. This damping characterization is believed to adequately reflect the light damping of the longer period modes (transverse and vertical stiffening truss modes, cable sway modes) and the heavier damping of lower period modes in supporting components.

Linear multi-support excitation time history analysis

Linear multi-support ground motion analyses were conducted to evaluate the effects of the time-delayed incoherent ground motions. These motions changed significantly the peak response of some critical components such as the truss chords and the tower bases, due to the additional structural modes that they excite and the change in phasing of various responses. These analyses also provided a reliable indication of the locations of significant nonlinearities in seismic response.

For the multi-support analyses, the equations of dynamic equilibrium were formed with respect to the inertial reference frame, in total displacement coordinates. Since all displacements, velocities, and accelerations were referenced to total displacement coordinates, no partitioning of the equations between total and relative terms was required, and all computed results were representative of total values, rather than the relative system of the uniform-support analyses. Therefore, interpretation of the results required some additional care.

The multi-support model was driven by the ground motions by applying "fictitious" force time histories at the interface nodes where the SSI-based impedances were assembled. These driving functions were derived by considering the stand-alone caisson motions from the SSI analyses as time-varying initial-strain loadings. As such, the computed caisson forces were adjusted to reflect this formulation.

Nonlinear multi-support excitation time history analysis

Final vulnerability estimates were based on nonlinear multi-support excitation analyses, which explicitly considered large displacements, joint pounding, tower-base rocking, and cable slackening. The nonlinear analyses provided a reasonable evaluation of seismic demands and vulnerability of the bridge. It is recognized, however, that incorporation of additional nonlinearities would provide an improved basis for determining the safety, serviceability, and retrofitting requirements of the structure.

The nonlinear response mechanisms were considered separately and in combination to gain an understanding of their contributions to seismic vulnerabilities. Some nonlinearities, such as suspender slackening that occurs in only a few locations, have little influence on vulnerability. Other nonlinearities, such as pounding of the back span cables on Bents A and B, have some local influence but little effect on global vulnerabilities. The most significant nonlinearities, such as joint pounding and P-Δ effects, have both local and global influences. Some additional static nonlinear studies were undertaken to qualitatively evaluate the effects of loss of truss member capacity on global behavior. These nonlinearities were not incorporated into the dynamic model.

Findings

The global analyses provided considerable insight into the seismic behavior of the bridge. The bridge was found to respond quite strongly over a wide frequency range, with significant demands in many superstructure and substructure components. The following observations are important in understanding its vulnerability:

1. The suspended system responds strongly in its relatively long-period fundamental mode; some higher-mode response is also apparent (Fig. 10). Some of the higher-mode participation is apparently due to multi-support excitation, which can excite traveling waves in the roadway. Forces in truss components appear to be dominated by the higher-mode, short wave-length traveling waves.

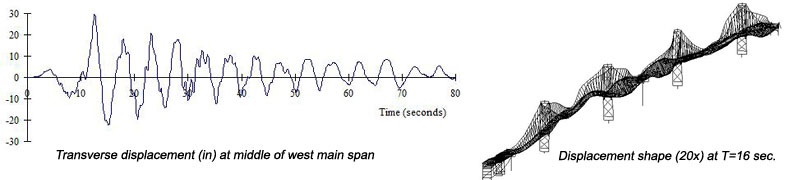
Fig. 10: Multi-support response of suspended system

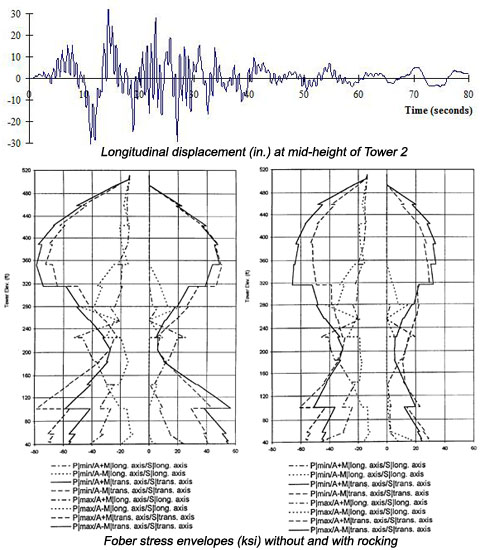
Fig. 11: Multi-support response of towers

2. Tower response is strongest at the higher frequency of the tower (Fig. 11). Tower demands are largely due to first longitudinal mode bending moments, with moment diagrams corresponding to behavior as a cantilever column, fixed at the caisson tops and propped by the elastic guy provided by the side-span cables. Rocking of the tower bases due to yielding of the anchor bolts partially decouples the bridge from the foundations, and therefore significantly reduces bending demands in the tower shafts. Impact between towers and the longer-period stiffening trusses appears to limit maximum longitudinal displacements of the towers, therefore limiting maximum curvatures and global fiber strains in the tower shafts.

3. Three-dimensional behavior of the unbraced double-deck stiffening truss system puts significant bending demands on the joints between the floor beams and the truss posts. Transverse racking (distortion) of the truss cross section causes many cycles of large bending demands about the longitudinal axes of truss posts and floor beams. The demands are critical at the connections between these two members that occur at each truss panel, where bending and shear capacity are provided primarily by the main gusset plates. Even at ¼ span , the bending demands are significantly higher than the capacity of about 400 ft-k. Global transverse shear in the truss cross section causes large bending moments about the vertical axes of the floor beams, which apparently act as stubs, feeding transverse shear forces into the relatively stiff floor slabs.

These global dynamic response analyses provided a reliable indication of the location and extent of damage that can be expected in the West Bay Crossing due to a major earthquake. Seismic vulnerability of bridge components was evaluated by comparing demands from these analyses with capacities, in accordance with the performance criteria. In a few instances, such as the truss post / floor beam connections discussed above, the vulnerability of the bridge to loss of functionality or safety could be better estimated by refined analyses that explicitly include additional nonlinear response mechanisms. Retrofitting measures required for the bridge to meet functionality and reparability criteria could also be refined on the basis of such studies.

Local Component Analyses

Structural components were analyzed prior to global analyses to provide input to global model development, as well as after the global analyses to evaluate their performance. Both computer solutions and detailed hand calculations were used in these analyses. A few of the more interesting studies are summarized here.

Foundations

Three-dimensional soil-structure interaction (SSI) analyses were conducted by Geomatrix using the computer program SASSI [9] for both pre- and post- global assessments. Caissons W-2 through W-6 were subjected to additional post-global check evaluations by OPAC using frame-element-and-dashpot models. The input rock motions were the multiple support motions developed previously to account for effects of spatially incoherent ground motions [3]. The SSI studies consisted of subsurface characterization, finite element modeling, development of impedance functions, development of input motions, and foundation demand / capacity evaluation.

Subsurface Characterization: Various clay layers up to 160 feet deep overlay Franciscan bedrock at the site. A layered soil idealization was developed at each pier location; strain-compatible properties for the layers were evaluated using the program SHAKE [10] to perform site response analyses with iteration on soil properties. Soil properties for the SHAKE analyses were based on published data for similar soils in the Bay Area.

Finite Element Models: Ten separate models were developed, each extending down to bedrock. Surrounding soils were idealized as semi-infinite viscoelastic layers; underlying rock was idealized as a viscoelastic half-space. Layer thickness was selected to capture the anticipated frequency range of soil response. The caissons and excavated soils were idealized as eight-node brick elements. An effective density and elastic modulus were used to account for the open cells of the caissons. Hydrodynamic effects were simulated using added masses.

Impedance Functions: Frequency-dependent impedances defined as K_ij ( ω) = k_ij (ω ) + i ωC_ij ( ω ) were developed for the six coupled DOF at an interface point on each foundation model. Frequency-independent masses and stiffnesses were developed for the global time-domain model by fitting polynomials of the form  k_ij (ω ) = (k_o)_ij - ω²(m_o)_ij to the real part of the impedances. Damping function polynomials of the form        I_ij = ω c_ij = A_ij + B_ij + C_ijω² + D_ijω³ were curve-fitted to the imaginary part. Good fits to the real parts suggest that the frequency-dependent stiffness is reasonably approximated by a static stiffness and a mass.

Motions: Histories of foundation accelerations, velocities, and displacements at each interface DOF were computed from the SSI analyses, for use in developing the driving functions for the global analysis. Input motions were taken as the rock accelerations generated in the Seismic Ground Motion Coherency Study [3].

Response: Foundation response was evaluated by driving the SSI models with the rock motions and the interface forces from the superstructure. As a check, simpler models consisting of frame elements for the caissons, springs for the bedrock, dashpots for the soil, and lumped masses for the water were evaluated under the same conditions. The two models provided time-histories and envelopes of demands over the height of the caissons.

Envelopes of transverse shear forces and longitudinal-axis moments in caisson W-4 are shown in Fig. 12. For all caissons, the SASSI and frame models agreed within about 20 percent.

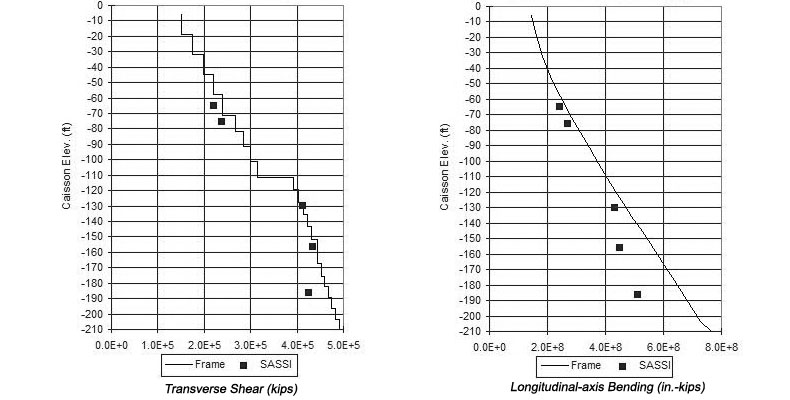
Fig. 12: Demand envelopes for caisson W-4

Vulnerability evaluation of the caissons was limited to comparing the shear and bending demands discussed above with corresponding capacities. The caissons are lightly reinforced with low-deformation bars; some light-gauge steel formwork supports left from construction clouded the capacity evaluation issues. Even considering this steel as fully effective, cracking moments were larger than ultimate moment capacities. The vulnerability conclusions were based on expressing shear demands as a function of √f'c and comparing them to limiting values between 2 (the ACI limit) and 6 (a value supported by some experiments but not in accordance with Caltrans retrofit criteria), and by comparing axial and bending demands with conventionally calculated P-M interaction surfaces. Such comparisons for the demands on W-4 are shown in Fig. 13. In interpreting this figure it is valuable to note that the natural period of this caisson is about ¼ second.

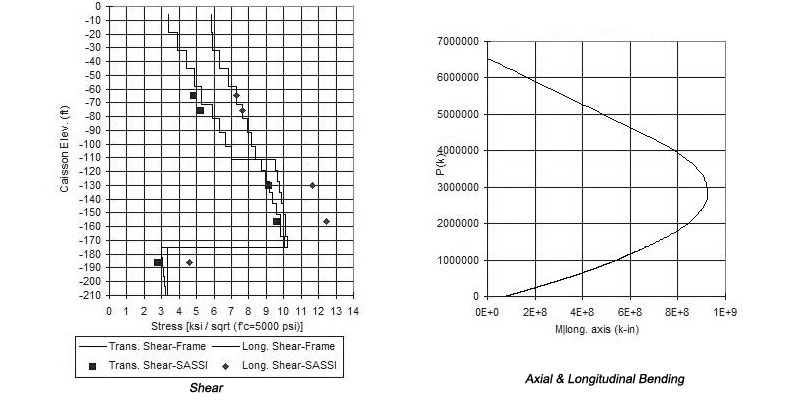
Fig. 13: Demand vs Capacity for caisson W-4

Stand-alone Tower Models

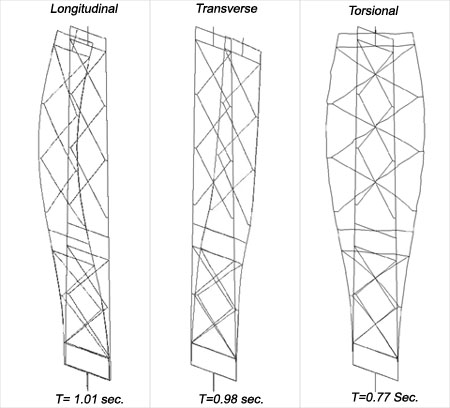
Fig. 14: Tower 2 Vibration modes

A model of Tower 2 was evaluated for vibration properties, dynamic response, and the effects of tower-base rocking. The tower and caisson models were taken directly from the global model. Inclined springs represented the elastic stiffness of the cable.

Vibration modes were extracted to determine how short a structural period is required to adequately capture mass participation of the tower. The first three vibration modes are illustrated in Fig. 14.

The computed vibration properties illustrated that fundamental tower modes fall in or near the plateau of the acceleration spectra for the evaluation earthquakes, suggesting that the towers will respond quite strongly to the ground motions. Also, it showed that consideration of vibration periods as short as ¼ second is necessary in order to capture 90% of the tower mass.

Tower Bases

An inelastic finite element model of the base of Tower 3 was analyzed to evaluate behavior, performance, and damage patterns as moments cause the edges of the tower base to uplift. It was also used to validate the filamented model used in global analyses. The model included explicit consideration of the base plate, anchor bolts, stiffening fins, vertical webs and bulkheads up to the third bulkhead, 21 ft above the base plate. Longitudinal rocking behavior was studied by loading the model with vertical dead load and then incrementing a rotation about the transverse axis.

The model was pushed to a deformation d/c ratio of about 3.0 (Fig. 15); a sharp drop in moment was observed at a system d/c ratio of 2.9 (0.0115 radians rotation). The drop in capacity appears to be associated with buckling of the fins, especially those at the corners. The 1.9% strains in the anchor bolts are far from fracture even at peak deformation. Inelastic rivet behavior was not modeled; at a few critical locations, however, rivet demand exceeded capacity by a factor of two. Plastic strains caused a permanent-set deformation after unloading. At a d/c ratio of 2.0 (the highest value from the global analysis), about 24.5' of the base plate uplifts (¾ of the base length), and fairly limited plate buckling was observed.

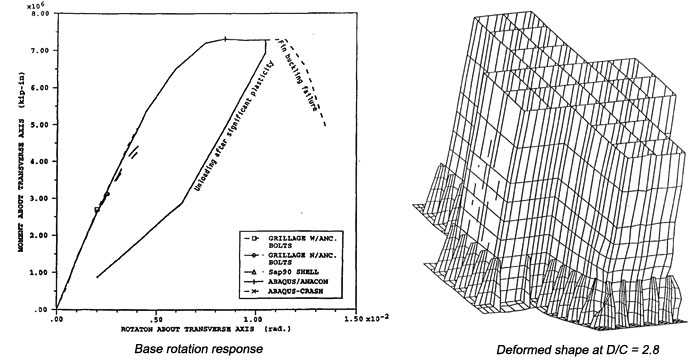
Fig. 15: Inelastic model of Tower 3 base region

Stiffening Trusses

A two-bay segment of the stiffening truss was studied to evaluate its inelastic system behavior in various deformation modes. A detailed inelastic model of side span panel points 17 to 19 (Fig. 16) was developed and evaluated under monotonic and cyclic deformations representative of various global actions.

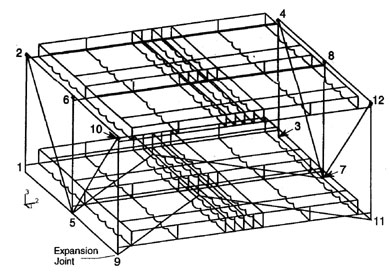
Fig. 16: Truss model

Truss members, floor beams, and braces were modeled with beam elements, using a cyclic material model that incorporates the Bauschinger effect and low cycle fatigue. Concrete slabs and stringers were modeled with two-dimensional orthotropic composite reinforced concrete plate elements. Connection offsets and eccentricities were also modeled. The model was capable of predicting member-level material and geometric nonlinear behavior, gross low cycle fatigue, and member buckling; but not highly localized buckling. It was felt that this model, combined with judgment and experience, was adequate to provide an initial prediction of the system ductility capacity.

Inelastic deformation characteristics, vulnerabilities, and ductility capacities of the trusses were investigated by subjecting this model to axial, torsion, distortion, horizontal flexure, vertical flexure, horizontal shear, vertical shear, and longitudinal distortion deformation patterns. For each deformation pattern, monotonic loadings provided estimates of the displacements at unit ductility, while cyclic loadings provided estimates of the ductility capacities in each deformation mode. Cyclic behavior is illustrated in Fig. 17 and discussed below.

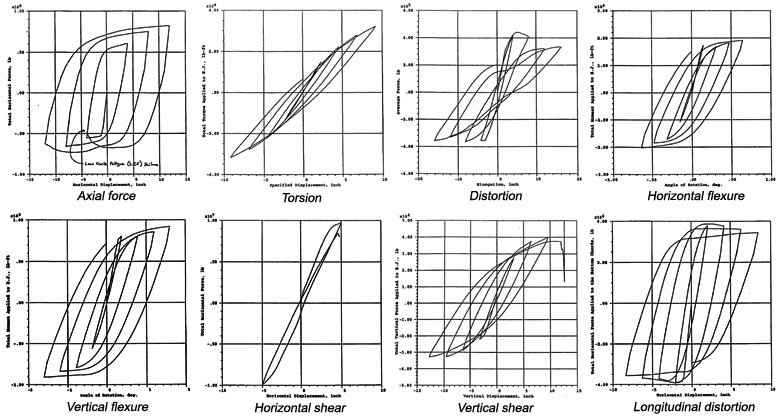
Fig. 17: Truss system inelastic deformation characteristics

The deformation patterns associated primarily with axial straining of the chords (e.g. axial, horizontal flexure, vertical flexure, and longitudinal distortion) are characterized by smooth, wide hysteresis loops and significant ductility capacity. The studies suggested system ductility capacities of 3 to 4 for these cases. The horizontal and vertical shear patterns are apparently governed by buckling of posts and diagonals. The studies suggested system ductility capacities of 1.5 to 2 for these cases. The torsion case has narrow hysteresis loops, it lacks a well-defined yield point and appears to be governed by geometric nonlinearity. The studies suggested system ductility capacities of about 3 for this case. The distortion case has narrow hysteresis loops of dramatically decreasing stiffness, indicative of progressive failure not associated with axial stress-strain. Resistance is primarily due to bending of the post-girder box frame. Failure was at a system ductility of about 3.

Vulnerability

The engineering studies conducted in the structural evaluation of the West Bay Crossing led to predictions of the following vulnerabilities to function-or safety- threatening damage in the maximum credible event:

1. The foundations of Piers W-2 through W-6 are subject to significant biaxial shear and moment demands. The effects of these demands could include some caisson rocking, shear and tension cracking of the concrete above and below the mud line, and spalling of concrete cover on both inside and outside surfaces.

2. Tower vulnerability is predicted at the bases (plate buckling and tension yield of the hold-down bolts), riveted splices (plate buckling and tension fracture), cable saddles (longitudinal shear), truss connections (pounding), and struts (longitudinal shear and bending). The cable bents are similarly vulnerable.

3. The suspended truss system is vulnerable to damage in transverse bending of the floor beams (due to global transverse shear), bending of the truss post joints (due to distortion), and buckling of the chords and diagonals (due to vertical and transverse system curvatures). Large transverse shears in the roadway slabs are also predicted, particularly in the unbraced upper chord plane. This truss damage may be correlated to loss of function, but probably not to overall stability problems since the cables carry all dead load.

4. The continuous trusses at the San Francisco Anchorage have transverse vulnerabilities similar to the suspended trusses. In addition, their bottom chords are under high demand near the fixed bearings on the Anchorage. The bearings and bents that support these spans are also under high demands.

5. The concrete piers, anchorage housings, and center anchorage are under high demands due to both overall shaking and local wall flexure. They are lightly reinforced, but their thick and compact walls may have some out-of-plane reserve strength due to internal arching action.

The suspenders, cables, and anchorages were found to be relatively unsusceptible to damage due to the evalua-tion ground motions. Slackening (or complete loss of tension) of the main cables is not predicted, and only in one incident do any suspenders slacken. Only some local slapping damage is predicted in the cables, where they enter the anchorage housings and pass through other steelwork.

Conclusions

A detailed seismic vulnerability evaluation was undertaken of the West Bay Crossing of the San Francisco - Oakland Bay Bridge. A primary objective of the engineering studies that were undertaken was to estimate the safety and functionality of the bridge in earthquakes of various probabilities. The assumptions, methods, and results of these components are summarized here.

Performance criteria addressed functionality, safety, and reparability. Component performance was expressed in terms of deformation capacities, which depend on the form, function, and behavior of the item.

Multi-support rock motions provided by Caltrans were used in the response analyses. The safety evaluation motions were representative of a Maximum Credible Event (Mw=8) on the San Andreas Fault.

Numerous local and global computer models were used to predict the seismic response and behavior of the bridge. Global models were used to evaluate overall behavior and demands. Local models were used to develop simplified global representations of subsystems, and to provide refined estimates of deformation capacities.

The global model represented the entire bridge from anchorage to anchorage, and was subjected to static and dynamic analyses to arrive at estimates of seismic demands and behavior of the bridge.

Local component analyses were performed of the foundations, towers, stiffening trusses, and other components in order to calibrate demands to damage and damage to vulnerability.

The bridge was found to be susceptible to some damage in both the safety evaluation and functional evaluation earthquakes.

Retrofit measures were identified by OPAC to address each of the vulnerabilities found in the evaluations. Retrofit engineering was undertaken by Caltrans and is outside the scope of this project.

References

1. Ketchum, M.A., Seismic Analysis of the Existing West Bay Spans of the San Francisco - Oakland Bay Bridge, Contract No. 59U064, prepared for Caltrans by OPAC Consulting Engineers, 1994.
2. Power, M., Seismic Ground Motion Study for West San Francisco Bay Bridge, Contract No. 59N772, prepared for Caltrans by Geomatrix Consultants, 1992.
3. Power, M., Seismic Ground Motion Coherency Study for West San Francisco Bay Bridge, Contract No. 59N772, prepared for Caltrans by Geomatrix Consultants, 1992.
4. Raab N.C., and Wood H.C., Earthquake Stresses in the San Francisco-Oakland Bay Bridge, ASCE Transactions, Paper No. 2123, v. 106, pp. 1363-1390, 1941.
5. Gates, J., Caltrans Seismic Performance Criteria Directive Memo, March 9, 1993.
6. Ivy, et al. Live Loading for Long-Span Highway Bridges, Transactions of the ASCE, Vol. 119, 1954.
7. Ketchum, M.A., Benicia-Martinez Bridge Preliminary Engineering Study, Segmental Concrete Box Girder Alternatives, Contract No. 59K051, prepared for Caltrans by T.Y. Lin International, 1990.
8. Carder, Dean S., Observed Vibration of Bridges, Bulletin of the Seismological Society of America, v. 27, no. 4, pp. 267-303, October 1937.
9. Lysmer, J., et al., SASSI - a system for analysis of soil-structure interaction, Report No. UCB/GT/81-02, Geotechnical Engineering, University of California, Berkeley, California, 1981.
10. Schnabel, P.B., et al., SHAKE - A computer program for earthquake response analysis of horizontally layered sites, Report No. UCB/EERC 71-12, EERC, University of California, Berkeley, December 1972.